Assumptions In Linear Regression
Table Of Contents:
- What Is A Parametric Model?
- Assumptions In Linear Regression.
(1) What Is A Parametric Model?
- Regression is a parametric approach.
- ‘Parametric’ means it makes assumptions about data for the purpose of analysis.
- Due to its parametric side, regression is restrictive in nature.
- It fails to deliver good results with data sets that don’t fulfill its assumptions.
- Therefore, for a successful regression analysis, it’s essential to validate these assumptions.
(2) Assumptions Of Linear Regression Model.
- Linear Relationship Between Input and Output.
- No Multicollinearity – No Linear Relationship Between Individual Variables.
- No Autocorrelation Of Error Terms.
- Homoscedasticity– Error Term Has Constant Variance.
- Mean Of Error Term Are Zero.
- Normal Distribution Of Error Terms.
- No Endogeneity – None Of Individual Variables Are Correlated With Error Term.
(1) Linear & Additive Relationship Between Input and Output.
- According to this assumption, the relationship between the independent and dependent variables should be linear.
- The reason behind this relationship is that if the relationship will be non-linear which is certainly the case in the real-world data then the predictions made by our linear regression model will not be accurate and will vary from the actual observations a lot.
- If you fit a linear model to a non-linear, non-additive data set, the regression algorithm would fail to capture the trend mathematically, thus resulting in an inefficient model.
- Also, this will result in erroneous predictions on an unseen data set.
How To Check:
- Look for residual vs fitted value plots (explained below).
- Also, you can include polynomial terms (X, X², X³) in your model to capture the non-linear effect.
- But still, you can check the linearity between the independent and dependent variables by plotting them as scatter plots.
- Scatter plots will give you a very good idea about the linearity of the variables.
- You will have to plot multiple scatter plots for each independent variable keeping the dependent variable constant.
Residual vs Fitted Plot:

- This scatter plot shows the distribution of residuals (errors) vs fitted values (predicted values).
- It is one of the most important plots which everyone must learn.
- It reveals various useful insights including outliers.
- The outliers in this plot are labeled by their observation number which makes them easy to detect.
There are two major things that you should learn:
- If there exists any pattern (maybe, a parabolic shape) in this plot, consider it a sign of non-linearity in the data. It means that the model doesn’t capture non-linear effects.
Solution:
- To overcome the issue of non-linearity, you can do a nonlinear transformation of predictors such as log (X), √X, or X² transform the dependent variable.
Example:

Super Note:
- By looking at the shape of the error you can guess what is the problem in the model.
- If you get the parabolic shape you can tell that your model is missing the nonlinearity to capture.
- If it has autocorrelation then you are missing an important variable.
- Linear Regression Models can’t capture non-linearity in the variables, they can only make the linear equation as it is designed for that.
- It’s like fitting a straight rod inside a circular pile it will never fit how much you try.
(2) No Multicollinearity
- It occurs when the independent variables show moderate to high correlations among themselves.
- In a model with correlated variables, it becomes a tough task to figure out the true relationship of predictors with the response variables.
- In other words, it becomes difficult to find out which variable is actually contributing to predicting the response variable.
- Additionally, when predictors are correlated, the estimated regression coefficient of a correlated variable depends on the presence of other predictors in the model.
- If this happens, you’ll end up with an incorrect conclusion that a variable strongly / weakly affects the target variable.
- Since, even if you drop one correlated variable from the model, its estimated regression coefficients would change.
- That’s not good!
How To Check:
Test-1: Correlation Matrix
- When computing the matrix of Pearson’s Bivariate Correlation among all independent variables the correlation coefficients need to be smaller than 1.
Test-2: Tolerance
- the tolerance measures the influence of one independent variable on all other independent variables; the tolerance is calculated with an initial linear regression analysis.
- Tolerance is defined as T = 1 – R² for these first step regression analysis.
- With T < 0.1 there might be multicollinearity in the data and with T < 0.01 there certainly is.
Test-3: Variance Inflation Factor (VIF)


- The variance inflation factor can estimate how much the variance of a regression coefficient is inflated due to multicollinearity.
- A Variance Inflation Factor (VIF) provides a measure of multicollinearity among the independent variables in a multiple regression model.
- Detecting multicollinearity is important because while multicollinearity does not reduce the explanatory power of the model, it does reduce the statistical significance of the independent variables.
- A large VIF on an independent variable indicates a highly collinear relationship to the other variables that should be considered or adjusted for in the structure of the model and selection of independent variables.
- The variance inflation factor of the linear regression is defined as VIF = 1/T.
- VIF value <= 4 suggests no multicollinearity whereas a value of >= 10 implies serious multicollinearity.
- Above all, a correlation table should also solve the purpose.
- The simplest way to address the problem is to remove independent variables with high VIF values.
Illness In The Model:
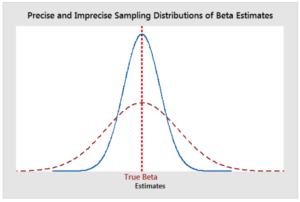
- Inefficiency Of Coefficients(Beta Values).
- Suppose, y = α + β1×1 + β2×2 + e
- if x1 and x2 are correlated, if x1 is increasing y should increase β1 times but, as x1 and x2 are correlated as x1 increases x2 will also increase and y will increase by β1 plus β2 times.
- Hence, now we can’t say if x1 is increasing y will increase by β1 times.
- Now β1 got inefficient, in Statistics which means the variance of β1 increases. Which is not good for the model.
- As the Gradient Descent will try to find out the correct β1 value so the error will be minimal, it will also try to consider the x2 changes.
- Hence the variability in β1 will increase.
Removals Of Multicollinearity:
- Remove some of the highly correlated independent variables.
- Linearly combine the independent variables, such as adding them together.
- LASSO and Ridge regression are advanced forms of regression analysis that can handle multicollinearity. I
- Partial least squares regression uses principal component analysis to create a set of uncorrelated components to include in the model.
- PCA is used when we want to reduce the number of variables in our data but we are not sure which variable to drop.
- It is a type of transformation that combines the existing predictors in a way that only keeps the most informative part.
- It then creates new variables known as Principal components that are uncorrelated.
- So, if we have 10-dimensional data then a PCA transformation will give us 10 principal components and will squeeze the maximum possible information in the first component and then the maximum remaining information in the second component, and so on.
- The primary limitation of this method is the interpretability of the results as the original predictors lose their identity and there is a chance of information loss.
- At the end of the day, it is a trade-off between accuracy and interpretability.
- Multicollinearity affects the coefficients and p-values, but it does not influence the predictions, precision of the predictions, and the goodness-of-fit statistics.
- If your primary goal is to make predictions, and you don’t need to understand the role of each independent variable, you don’t need to reduce severe multicollinearity.
(3) No Autocorrelation Of Error Terms.
- The presence of correlation in error terms drastically reduces model’s accuracy.
- This usually occurs in time series models where the next instant is dependent on previous instant.
- If the error terms are correlated, the estimated standard errors tend to underestimate the true standard error.
- If this happens, it causes confidence intervals and prediction intervals to be narrower.
- Narrower confidence interval means that a 95% confidence interval would have lesser probability than 0.95 that it would contain the actual value of coefficients.
- Let’s understand narrow prediction intervals with an example:
- For example, the least square coefficient of X¹ is 15.02 and its standard error is 2.08 (without autocorrelation).
- But in presence of autocorrelation, the standard error reduces to 1.20. As a result, the prediction interval narrows down to (13.82, 16.22) from (12.94, 17.10).
- Also, lower standard errors would cause the associated p-values to be lower than actual. This will make us incorrectly conclude a parameter to be statistically significant.
How To Check:
- Look for Durbin – Watson (DW) statistics. It must lie between 0 and 4.
- If DW = 2, implies no autocorrelation,
- 0 < DW < 2 implies positive autocorrelation
- while 2 < DW < 4 indicates negative autocorrelation.
- Also, you can see residual vs. time plots and look for the seasonal or correlated pattern in residual values.
Illness In The Model:
- Autocorrelation is one of the most important assumptions of Linear Regression.
- The dependent variable ‘y’ is said to be auto-correlated when the current value of ‘y; is dependent on its previous value.
- In such cases, the R-Square (which tells us how well our model is performing) is said to make no sense.
- We build a model so that given our independent variables we can detect how the dependent variable will move, but If the current month’s ‘y’ is dependent upon the previous month’s ’y’ then our model becomes non-robust.
- It is like saying if today it has rained tomorrow also it will rain.
- If today’s stock price is increasing tomorrow’s price will also increase.
- Then our model will be useless because there will be no need to consider all the independent variables in our model.
- We can only see the previous day’s value and can predict tomorrow’s value.
- Then it will come as a time series analysis, not a linear regression analysis.
(4) Homoscedasticity
- The presence of non-constant variance in the error terms results in heteroskedasticity.
- Generally, non-constant variance arises in presence of outliers or extreme leverage values.
- Look like, these values get too much weight, thereby disproportionately influences the model’s performance.
- When this phenomenon occurs, the confidence interval for out of sample prediction tends to be unrealistically wide or narrow.
How To Check:
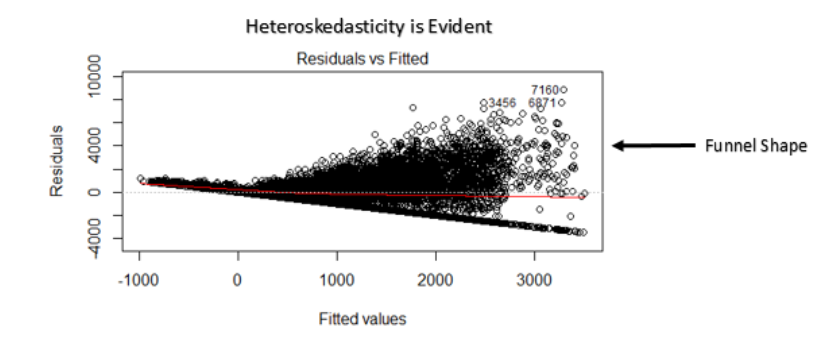
- You can look at residual vs fitted values plot.
- If heteroskedasticity exists, the plot would exhibit a funnel shape pattern (shown in next section).
- Also, you can use Breusch-Pagan / Cook – Weisberg test or White general test to detect this phenomenon.
Note:
- If a funnel shape is evident in the plot, consider it as the signs of non constant variance i.e. heteroskedasticity.
- To overcome heteroskedasticity, a possible way is to transform the response variable such as log(Y) or √Y. Also, you can use weighted least square method to tackle heteroskedasticity.
(5) Mean Of Error Term Is Zero
- The expected value of error should be zero.
- E(e) = 0
- Suppose we have a model, y = α+ βx + e
- People generally think that if you take an average of all the residuals it will automatically come to zero.
- But it will not always be the case. The average of the error terms will not always come to zero.
- Why we are making this assumption because, Suppose take this equation,
- y = α+ βx + 10
- Here the average value of the error is 10 which means, the estimated and the actual value of the prediction will never be the same, or will never come closer.
- It will always be off by a value of 10. That will not be a good model.
- That’s why we need to assume the average error term should be zero.
Solution:
- The constant term in the model will make the error term zero if it is not zero.
- y = α+ βx + 10
- Here the constant term is (α).
- For example, take an equation,
- y = 10+ βx + 3
- To make the error term here 3 to zero, we have to subtract and add 3 of the right side of the equation.
- y = 10+ βx + 3 + (3 – 3)
- Now the new equation will be,
- y = (10+3)+ βx + (3 – 3)
- y = (13)+ βx + (0)
- Here the error term has come to zero as the constant has taken care of it.
- When you are running your regression model with a constant term the error will automatically come to zero.
(6) Normal Distribution Of Error Terms.
- If the error terms are non-normally distributed, confidence intervals may become too wide or narrow.
- Once the confidence interval becomes unstable, it leads to difficulty in estimating coefficients based on the minimization of least squares.
- The presence of non–normal distribution suggests that there are a few unusual data points that must be studied closely to make a better model.
How To Check:
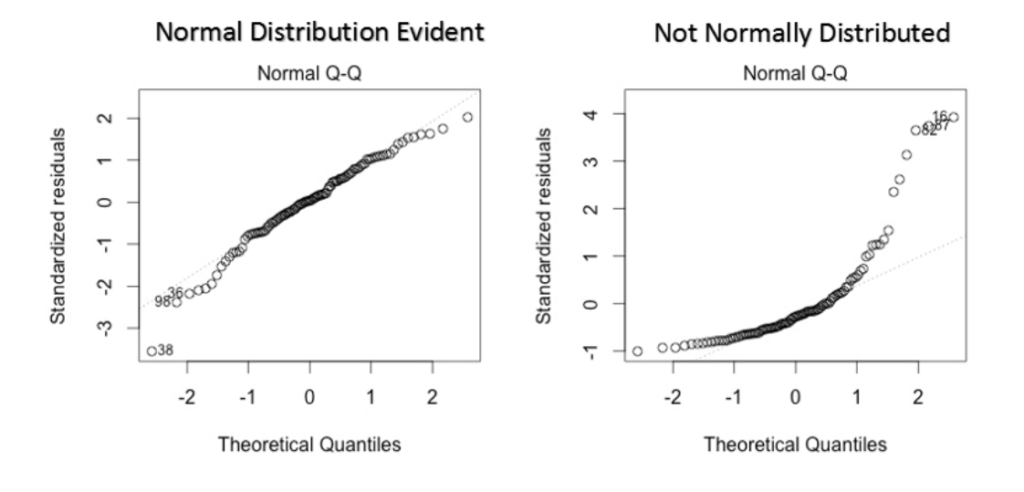
- You can look at QQ plot (shown below). You can also perform statistical tests of normality such as Kolmogorov-Smirnov test, Shapiro-Wilk test.
Note:
- This q-q or quantile-quantile is a scatter plot which helps us validate the assumption of normal distribution in a data set. Using this plot we can infer if the data comes from a normal distribution. If yes, the plot would show fairly straight line. The straight lines shows the absence of normality in the errors.
- If you are wondering what is a ‘quantile’, here’s a simple definition: Think of quantiles as points in your data below which a certain proportion of data falls. Quantile is often referred to as percentiles. For example: when we say the value of 50th percentile is 120, it means half of the data lies below 120.
Solution:
- If the errors are not normally distributed, non – linear transformation of the variables (response or predictors) can bring improvement in the model.
(7) No Endogeneity
- There is no relationship between the errors and the independent variables.
- Suppose we have a model, y = α+ βx + e
- Consider there exists a relationship between ‘x’ and ‘e’, if ‘x’ increases then ‘e’ will also increase.
- Here ‘x’ and ‘e’ are simultaneously moving together which means the effect of ‘x’ on ‘y’ seems quite substantial or more.
- But this is actually not the case. Because if ‘x’ is increasing ‘e’ is also increasing.
- Error effect will show in ‘x’ coefficient only, hence ‘β‘ will seem more significant. Which is not good.

